O Level CS P1 Hardware and Software Logic Gates
To view other notes of GCSE \ IGCSE Computer Science Click Here.
Logic gates serve as the building blocks to digital logic circuits using combinational logic. Many electronic circuits operate using binary logic gates. Logic gates basically process signals which represent true or false or the equivalent i.e. ON or OFF, 1 or 0
Whilst there are a number of logic gates, only the six simplest are covered in this booklet:
1. NOT gate
2. AND gate
3. OR gate
4. NAND gate
5. NOR gate
6. XOR gate.
The following notes describe the function of all six gates, how to produce truth tables, how to design networks using logic gates, and how to determine the output from a logic network
The six main logic gates
The most common symbols used to represent logic gates are shown below. To avoid confusion the graphical representations will be used in exam questions but candidates may use either set of symbols when answering questions.
Simple graphical representation
Symbol used to represent logic gates

A Truth Table is simply a table listing all the combinations of inputs and their respective outputs.
The NOT gate has only one input, but the rest have 2 inputs.
The next section describes the function of all six logic gates.
| Name | Symbol | Logic | Truth Table | |||||||||||||||
| NOT Gate |  | The output (called X) is true (i.e. 1 or ON) when the INPUT A is NOT TRUE (i.e. 0 or OFF) |
| |||||||||||||||
| AND Gate |  | The output is only true (i.e. 1 or ON) when the (INPUT A AND INPUT B) are both TRUE (i.e. 0 or OFF) |
| |||||||||||||||
| OR Gate |  | The output is true (i.e. 1 or ON) when the (INPUT A OR INPUT B) are TRUE (i.e. 0 or OFF) |
| |||||||||||||||
| NAND Gate | 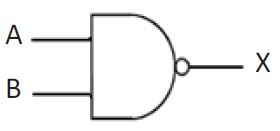 | This is basically an AND gate with the output inverted. The output is true (i.e. 1 or ON) when the (INPUT A AND INPUT B) are NOT both TRUE (i.e. 0 or OFF) |
| |||||||||||||||
| NOR Gate | This is basically an OR gate with the output inverted. The output is true (i.e. 1 or ON) if NOT (INPUT A AND INPUT B) are TRUE. |
| ||||||||||||||||
| Exclusive-OR Gate (XOR Gate) | The output is true only when the inputs are opposite of each other. |
|
Combinations of logic gates
Producing the truth table from a given logic network

If we now look at the output in two stages. First let us consider the outputs being produced at stages “S” and “T”. To do this, we need to draw a truth table. There are three inputs (A, B and C) which gives 23 (i.e. 8) possible combinations of 1s and 0s. To work out the outputs at “S” and “T” we need to refer to the truth tables for the NOR gate and for the AND gate. For example, when A = 1 and B = 1 then we have 1 NOR 1 which gives the value of S = 0. Continuing doing the same thing for all 8 possible inputs we get the following interim truth table.
The Final Stage involves S OR T
| A | B | C | S | T |
| 1 | 1 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 0 | 0 | 1 | 0 |
| S | T | X |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
| 0 | 0 | 0 |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 1 | 0 | 1 |
| A | B | C | X |
| 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 1 |
Designing logic networks to solve a specific problem and testing using truth tables
Consider the following problem:
“If button A or button B are on and button C is off then the alarm X goes on”
We can convert this into logic gate terminology (ON = 1 and OFF = 0):
If (A = 1 OR B = 1) AND (C = NOT 1) then (X = 1)
(Notice: rather than write 0 we use NOT 1)
To draw the logic network, we do each part in brackets first i.e. A = 1 OR B = 1 is one gate then C = NOT 1 is the second gate. These are then joined together by the AND gate. Once the logic network is drawn we can then test it using a truth table. Remember the original problem – we are looking for the output to be 1 when A or B is 1 and when C is 0. Thus we get the following logic network and truth table from the network. Looking at the values in the truth table, we will be able to clearly see that it matches up with the original problem which then gives us confidence that the logic network is correct.

| A | B | C | X |
| 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 |
Let us now consider a second problem:
A steel rolling mill is to be controlled by a logic network made up of AND, OR and NOT gates only. The mill receives a stop signal (i.e. S = 1) depending on the following input bits:
| INPUT | BINARY VALUE | CONDITION |
| L | 1 0 | Length > 100 meters Length =< 100 meters |
| T | 1 0 | Temperature > 1000 C Temperature =< 1000 C |
| V | 1 0 | Velocity > 10 m/s Velocity =< 10 m/s |
A stop signal (S = 1) occurs when:
Either Length, L > 100 meters and Velocity, V < 10 m/s
Or Temperature, T < 1000 C and Velocity, V > 10 m/s
Draw a logic network and truth table to show all the possible situations when the stop signal could be received.
The first thing to do is to try and turn the question into a series of logic gates and then the problem becomes much simplified.
- The first statement can be re-written as: (L = 1 AND V = NOT 1) since Length > 100 meters corresponds to a binary value of 1 and Velocity < 10 m/s corresponds to a binary value of 0 (i.e. NOT 1).
- The second statement can be re-written as (T = NOT 1 AND V = 1) since Temperature < 1000C corresponds to a binary value of 0 (i.e. NOT 1) and Velocity > 10 m/s corresponds to a binary value of 1
- Both these statements are joined together by OR which gives us the logic statement: if (L = 1 AND V = NOT 1) OR (T = NOT 1 AND V = 1) then S = 1
We can now draw the logic network and truth table to give the solution to the original problem (input L has been put at the bottom of the diagram just to avoid crossing over of lines; it merely makes it look neater and less complex and isn’t essential):

| L | T | V | S |
| 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 0 |


